Omkrets

En sirkel med diameter lik 1 har en omkrets lik π.

Omkretsen av denne sirkelen er lengden av den svarte linjen.

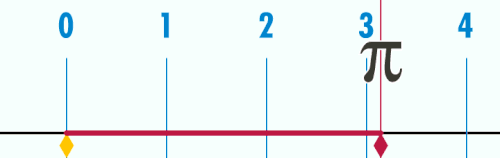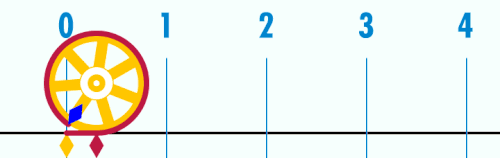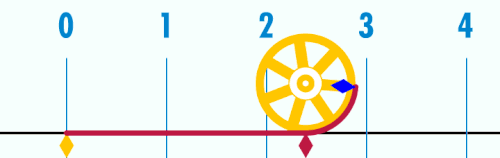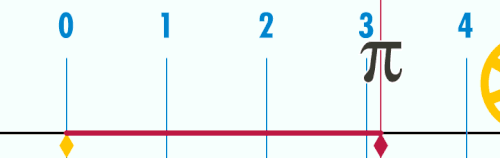
Omkrets er lengden av en lukket kurve. Omkretsen av et to-dimensjonalt område er lik lengden av områdets begrensning.

For mangekantede figurer i planet gjelder at omkretsen er lik summen av alle sidene. For sirkler med radius lik r er omkretsen lik 2πr. Enkelte geometriske figurer, som fraktaler, har uendelig omkrets.

Figurer som har samme omkrets kalles isoperimetriske.

Formler for omkrets

Form	Omkrets	Variable
Kvadrat	$O=4s$	s er lengden til alle sidene til kvadraten.
Rektangel	$O=2(l+b)$	l og b er lengde og bredde av rektangelet, det vil si lengden til sidene.
Trekant	$O=s_{1}+s_{2}+s_{3}$	sn er lengden til side nr. n i trekanten.
Sirkel	$O=2\pi r$   eller   $\ O=\pi d$	r er radien i sirkelen og d er diameteren.

Se også

• Areal

Denne artikkelen er en spire. Du kan hjelpe Wikipedia ved å utvide den.

Autoritetsdata